某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人，将这l6人的数学成绩编成茎叶图，如图所示．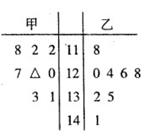
(I)茎叶图中有一个数据污损不清(用△表示)，若甲班抽出来的同学平均成绩为l22分，试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍，请将所有可能的结果列举出来，并求选出的两位同学不在同一个班的概率．
相关试题
在坐标轴上，离心率为
，且过点（4，-
）
的面积。
有两个不等的负根，q:方程
无实根，若p或q为真，p且q为假，求m的取值范围。
定圆
动圆M与定圆
都外切，求动圆圆心M的轨迹方程。
，若非p是q的充分不必要条件，求a的取值范围。
的椭圆的标准方程
，求椭圆方程。相关知识点
推荐套卷
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人，将这l6人的数学成绩编成茎叶图，如图所示．
(I)茎叶图中有一个数据污损不清(用△表示)，若甲班抽出来的同学平均成绩为l22分，试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍，请将所有可能的结果列举出来，并求选出的两位同学不在同一个班的概率．
粤公网安备 44130202000953号