如图，斜率为1的直线过抛物线
的焦点F，与抛物线交于两点A，B，
（1）若|AB|=8，求抛物线
的方程；
（2）设C为抛物线弧AB上的动点（不包括A，B两点），求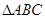
的面积S的最大值；
（3）设P是抛物线上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）
=
,求证：a+
，则
在R上是增函数；
，则
ABC是
；
的最小值为
；
，则A=B；
，则
，
、
，求
的值？推荐套卷
如图，斜率为1的直线过抛物线的焦点F，与抛物线交于两点A，B，
（1）若|AB|=8，求抛物线的方程；
（2）设C为抛物线弧AB上的动点（不包括A，B两点），求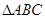的面积S的最大值；
（3）设P是抛物线上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值（仅与p有关）
粤公网安备 44130202000953号