设 是各项均为非零实数的数列
是各项均为非零实数的数列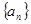 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上:
命题 :
: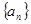 是等差数列;命题
是等差数列;命题 :等式
:等式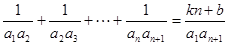 对任意
对任意 (
( )恒成立,其中
)恒成立,其中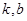 是常数。
是常数。
⑴若 是
是 的充分条件,求
的充分条件,求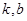 的值;
的值;
⑵对于⑴中的 与
与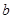 ,问
,问 是否为
是否为 的必要条件,请说明理由;
的必要条件,请说明理由;
⑶若 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
( )和正数M,数列
)和正数M,数列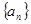 满足条件
满足条件 ,试求
,试求 的最大值。
的最大值。
推荐套卷
设 是各项均为非零实数的数列
是各项均为非零实数的数列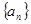 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上:
命题 :
: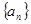 是等差数列;命题
是等差数列;命题 :等式
:等式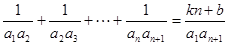 对任意
对任意 (
( )恒成立,其中
)恒成立,其中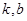 是常数。
是常数。
⑴若 是
是 的充分条件,求
的充分条件,求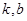 的值;
的值;
⑵对于⑴中的 与
与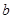 ,问
,问 是否为
是否为 的必要条件,请说明理由;
的必要条件,请说明理由;
⑶若 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
( )和正数M,数列
)和正数M,数列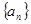 满足条件
满足条件 ,试求
,试求 的最大值。
的最大值。