（本小题共14分）
如图所示多面体中，AD⊥平面PDC，ABCD为平行四边形，E，F分别为AD，BP的中点，AD=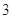
，AP=
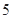，PC=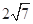
.
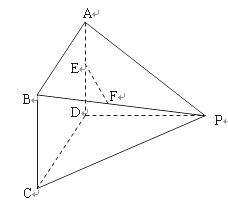
（Ⅰ）求证：EF∥平面PDC；
（Ⅱ）若∠CDP＝90°，求证BE⊥DP;
（Ⅲ）若∠CDP＝120°，求该多面体的体积.
是可导函数）
；（2）
；（2）
；
；（4）
。
的导数
在点
处可导，则函数
，判断
在
处是否可导？推荐套卷
（本小题共14分）
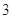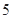如图所示多面体中，AD⊥平面PDC，ABCD为平行四边形，E，F分别为AD，BP的中点，AD=，AP=，PC=.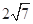
（Ⅰ）求证：EF∥平面PDC；
（Ⅱ）若∠CDP＝90°，求证BE⊥DP;
（Ⅲ）若∠CDP＝120°，求该多面体的体积.
粤公网安备 44130202000953号