如图,圆O与离心率为 的椭圆T:
的椭圆T: (
(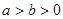 )相切于点M
)相切于点M 。
。
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线 、
、 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为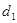 、
、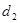 ,求
,求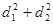 的最大值;
的最大值;
②若 ,求
,求 与
与 的方程。
的方程。
相关知识点
推荐套卷
如图,圆O与离心率为 的椭圆T:
的椭圆T: (
(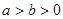 )相切于点M
)相切于点M 。
。
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线 、
、 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为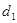 、
、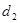 ,求
,求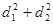 的最大值;
的最大值;
②若 ,求
,求 与
与 的方程。
的方程。