如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记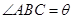 ,
,
(1)问当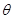 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。
相关知识点
推荐套卷
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记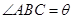 ,
,
(1)问当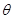 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。