在等差数列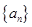 和等比数列
和等比数列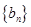 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 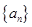 的前20项和S20=230.
的前20项和S20=230.
(Ⅰ)求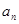 和
和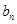 ;
;
(Ⅱ)现分别从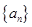 和
和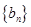 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
推荐套卷
在等差数列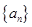 和等比数列
和等比数列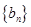 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 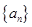 的前20项和S20=230.
的前20项和S20=230.
(Ⅰ)求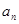 和
和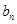 ;
;
(Ⅱ)现分别从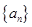 和
和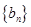 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.