如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC.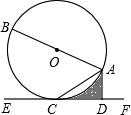 
（1）求证：EF是⊙O的切线；
（2）求证：AC2=AD·AB；
（3）若⊙O的半径为2，∠ACD=300，求图中阴影部分的面积．
相关知识点
推荐套卷
如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC.
（1）求证：EF是⊙O的切线；
（2）求证：AC2=AD·AB；
（3）若⊙O的半径为2，∠ACD=300，求图中阴影部分的面积．
粤公网安备 44130202000953号