今年5月10日,《重庆日报》刊登了一篇名为“重庆八中——用阅读的力量行走世界”的文章,报道了我校开展阅读教育的基本情况,文章同时被人民网、中国日报网等网络媒体转载.校文学社为了了解我校初三年级学生每周在阅览室阅读的时间,采用随机抽样的方法进行了问卷调查,调查结果分为“1小时以内”、“1小时~2小时”、“2小时~3小时”、“3小时~4小时”和“4小时以上”五个等级,分别用A、B、C、D、E表示,根据调查结果绘制成了如图所示的两幅不完整的统计图.由图中所给出的信息解答下列问题:

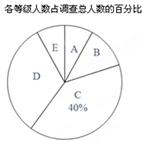
(1)校文学社共调查了_______名初三年级的同学,请将不完整的条形统计图补充完整;
(2)估计该年级2000名学生中,每周在阅览室阅读的时间为“1小时~2小时”的有____人;
(3)在此次调查活动中,初三年级甲班、乙班各有2人每周在阅览室阅读的时间都是4小时以上,报社记者想从中任选2人采访.用列表或画树状图的方法求选出的2人均来自甲班的概率.