某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x |
50 |
60 |
90 |
120 |
| y |
40 |
38 |
32 |
26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
相关知识点
推荐套卷
 球、体操课.学生可根据自己的爱好任选其中一项,老师
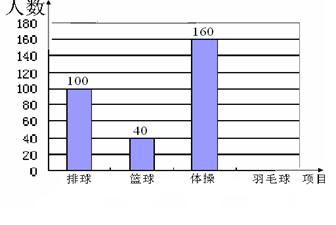
球、体操课.学生可根据自己的爱好任选其中一项,老师 根据学生报名情况进行了统计,并绘制了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
根据学生报名情况进行了统计,并绘制了右边尚未完成的扇形统计图和频数分布直方图,请你结合图中的信息,解答下列问题:
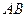 是
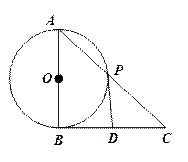
是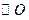 的直径,
的直径,
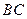 切
切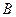 ,
,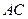 交
交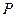 ,
,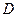 为
为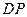 .
. 是
是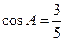 ,
,
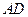 ∥
∥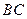 ,
, ,
,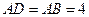 ,
,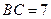 ,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点
,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点 处.
处.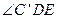 的度数;
的度数; 的面积.
的面积.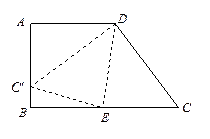
 中,一次函数
中,一次函数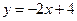 的图象分别与
的图象分别与 轴交于点A、 B,点
轴交于点A、 B,点 在
在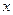 轴上,若
轴上,若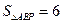 ,求直线PB的函数解析式.
,求直线PB的函数解析式.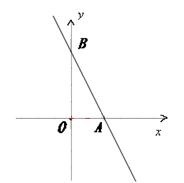
 粤公网安备 44130202000953号
粤公网安备 44130202000953号