已知二次函数y=ax2+bx+c（a≠0）的图象经过点（1，0），（5，0），（3，﹣4）．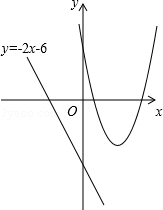
（1）求该二次函数的解析式；
（2）当y＞﹣3，写出x的取值范围；
（3）A、B为直线y=﹣2x﹣6上两动点，且距离为2，点C为二次函数图象上的动点，当点C运动到何处时△ABC的面积最小？求出此时点C的坐标及△ABC面积的最小值．
，求代数式
的值．
，其中
．
（2）
（2）
相关知识点
推荐套卷
已知二次函数y=ax2+bx+c（a≠0）的图象经过点（1，0），（5，0），（3，﹣4）．
（1）求该二次函数的解析式；
（2）当y＞﹣3，写出x的取值范围；
（3）A、B为直线y=﹣2x﹣6上两动点，且距离为2，点C为二次函数图象上的动点，当点C运动到何处时△ABC的面积最小？求出此时点C的坐标及△ABC面积的最小值．
粤公网安备 44130202000953号