甲、乙两车分别从A，B两地同时出发相向而行．并以各自的速度匀速行驶，甲车途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）直接写出a，m，n的值；
（2）求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；
（3）当两车相距120千米时，乙车行驶了多长时间？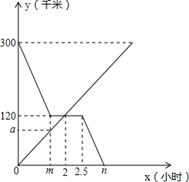
相关试题
与
，
，
， 0．七年级一班某次数学测验的平均成绩为80分，数学老师以平均成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分？
如图两个椭圆分别表示正数集合和整数集合（1）请在每个圈内填入6个数；（2）其中有3个数既是正数又是整数这3个数应填在______处（A，B，C）你能说出两个圈重叠部分表示什么数的集合吗？
相关知识点
推荐套卷
粤公网安备 44130202000953号