已知集合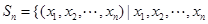 是正整数
是正整数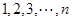 的一个排列
的一个排列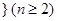 ,函数
,函数 对于
对于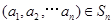 ,定义:
,定义: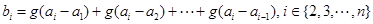 ,
, ,称
,称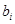 为
为 的满意指数.排列
的满意指数.排列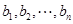 为排列
为排列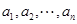 的生成列;排列
的生成列;排列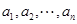 为排列
为排列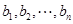 的母列.
的母列.
(Ⅰ)当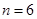 时,写出排列
时,写出排列 的生成列及排列
的生成列及排列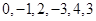 的母列;
的母列;
(Ⅱ)证明:若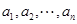 和
和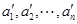 为
为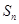 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于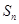 中的排列
中的排列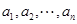 ,定义变换
,定义变换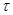 :将排列
:将排列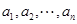 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换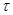 将排列
将排列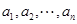 变换为各项满意指数均为非负数的排列.
变换为各项满意指数均为非负数的排列.
相关知识点
推荐套卷
 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与直线
与直线 的距离;
的距离; (
( )的距离为
)的距离为 ,直线
,直线 ,求
,求 的最小值.
的最小值. 中,点
中,点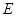 是
是 的中点,点
的中点,点 是
是 的中点,将△
的中点,将△ 、△
、△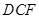 分别沿
分别沿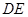 、
、 折起,使
折起,使 、
、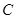 两点重合于点
两点重合于点 ,连接
,连接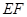 ,
,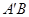 .
.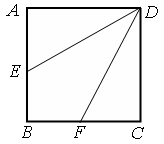

 ;
; 的余弦值.
的余弦值.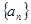 的前
的前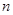 项和为
项和为 ,数列
,数列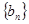 的首项
的首项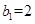 ,且点
,且点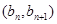 在直线
在直线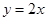 上.
上. ,求数列
,求数列 的前
的前 .
.
 ,求
,求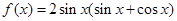 .
.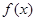 的最小正周期;
的最小正周期;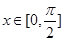 时,求
时,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号