有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t变化的函数关系.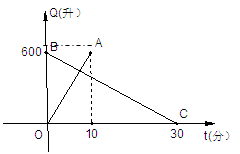
(1)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(2)现已知容器内有水200升,先打开两个进水管和一个出水管一段时间,然后再关上一个进水管,直至把容器放满水,若总共用时不超过8分钟。请问,在这个过程中同时打开两个进水管和一个出水管的时间至少是多少分钟?
相关知识点
推荐套卷
 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
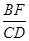 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号