某车间的甲、乙两名工人分别同时生产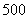
只同一型号的零件，他们生产的零件
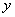（只）与生产时间
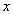的函数关系的图象如图所示。根据图象提供的信息解答下列问题：
（1）甲每分钟生产零件_______只；乙在提高生产速度之前已生产了零件_______只；
（2）若乙提高速度后，乙的生产速度是甲的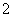
倍，请分别求出甲、乙两人生产全过程中，生产的零件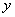（只）与生产时间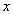的函数关系式；
（3）当两人生产零件的只数相等时，求生产的时间；并求出此时甲工人还有多少只零件没有生产．
相关试题
如图，点D是线段AB的中点，点C是线段AB的垂直平分线上的任意一点，DE⊥AC于点E，DF⊥BC于点F．
（1）求证：CE=CF；
（2）点C运动到什么位置时，四边形CEDF成为正方形？请说明理由．
=
-3⑵ 解不等式组：
＋(－1)0+
如图，已知二次函数y=a（x2-6x+8）(a>0)的图象与x轴交于点A、B两点，与y轴交于点C．
（1）求A、B两点的坐标；
（2）若S△ABC=8，则过A、B、C三点的圆是否与抛物线有第四个交点D？若存在，求出D点坐标；若不存在，说明理由．
（3）将△OAC沿直线AC翻折，点O的对应点为O＇．
①若O＇落在该抛物线的对称轴上，求实数a的值；
②是否存在正整数a，使得点O＇落在△ABC的内部，若存在，求出整数a的值；若不存在，请说明理由．
相关知识点
推荐套卷
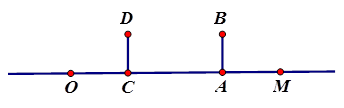
粤公网安备 44130202000953号