某商场共五层,从五层下到四层有3个出口,从三层下到二层有4个出口,从二层下到一层有4个出口,从一层走出商场有6个出口。安全部门在每层安排了一名警员值班,负责该层的安保工作。假设每名警员到该层各出口处的时间相等,某罪犯在五楼犯案后,欲逃出商场,各警员同时接到指令,选择一个出口进行围堵。逃犯在每层选择出口是等可能的。已知他被三楼警员抓获的概率为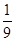 。
。
(Ⅰ)问四层下到三层有几个出口?
(Ⅱ)天网恢恢,疏而不漏,犯罪嫌疑人最终落入法网。设抓到逃犯时,他已下了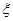 层楼,写出
层楼,写出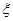 的分布列,并求
的分布列,并求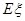 。
。
相关知识点
推荐套卷
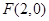 和定直线
和定直线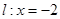 ,动点与定点
,动点与定点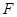 的距离等于点
的距离等于点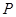 到定直线
到定直线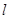 的距离,记动点
的距离,记动点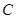 .
.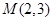 为圆心的圆与曲线
为圆心的圆与曲线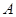 、
、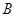 不同两点,且线段
不同两点,且线段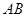 是此圆的直径时,求直线
是此圆的直径时,求直线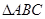 中,角
中,角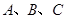 所对的边分别为
所对的边分别为 ,已知
,已知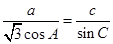 ,
,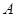 的大小;
的大小;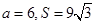 ,求
,求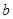 和
和 的值.
的值.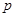 :方程
:方程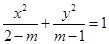 表示的曲线是焦点在y轴上的双曲线,命题
表示的曲线是焦点在y轴上的双曲线,命题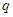 :方程
:方程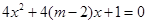 无实根,若
无实根,若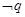 为真,求实数
为真,求实数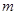 的取值范围.
的取值范围.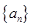 的前n项和
的前n项和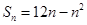
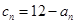 ,求数列
,求数列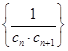 的前
的前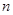 项和
项和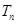 .
. M为CD的中点.
M为CD的中点.
 ,使
,使 ,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
,且P点到A、B 的距离和为定值,求点P的轨迹E的方程; 的直线与轨迹E交于P、Q两点,求
的直线与轨迹E交于P、Q两点,求 面积的最大值.
面积的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号