| A.(几何证明选讲选做题)
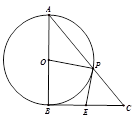 |
| B.(矩阵与变换选做题) 已知M=  ,N= ,N=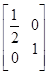 ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. |
| C.(坐标系与参数方程选做题) 在平面直角坐标系xOy中,直线m的参数方程为  (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. (t为参数);在以O为极点、射线Ox为极轴的极坐标系中,曲线C的极坐标方程为ρsinθ=8cosθ.若直线m与曲线C交于A、B两点,求线段AB的长. |
| D.(不等式选做题) |
设x,y均为正数,且x>y,求证:2x+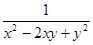 ≥2y+3.
≥2y+3.
相关知识点
推荐套卷
 .(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q=
.(1)求直线A1C与D1C1所成角的正切值;(2)在线段A1C上有一点Q,且C1Q= C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
C1A1,求平面QDC与平面A1DC所成锐二面角的大小.
 在y轴右侧的第一个最大值点和最小值点,O为原点,若
在y轴右侧的第一个最大值点和最小值点,O为原点,若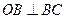 ,且
,且 (1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间
(1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间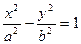 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足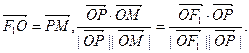 (Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点
(Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点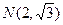 ,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求
,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求 时,直线AB的方程.
时,直线AB的方程.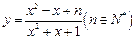 的最小值为
的最小值为 ,最大值为
,最大值为 ,又
,又
 的通项公式;
的通项公式; ,求
,求 的值;
的值; ,是否存在最小的整数
,是否存在最小的整数 ,使对
,使对 ,有
,有 成立?若存在,求出
成立?若存在,求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号