(本题满分14分) 若F1、F2为双曲线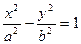
的左、右焦点，O为坐标原点，P在双曲线左支上，M在右准线上，且满足
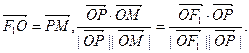（Ⅰ）求此双曲线的离心率；（Ⅱ）若此双曲线过点
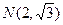，求双曲线方程；（Ⅲ）设（Ⅱ）中双曲线的虚轴端点为B1，B2（B1在y轴正半轴上），求B2作直线AB与双曲线交于A、B两点，求
时，直线AB的方程.
有两个不同的交点,求证:
，求证：
。
，
，求
的最大值。
上的两动点，且满足与圆内一定点
，使
，求过Ｐ和Ｑ的两条切线的交点M的轨迹。
上的最小值为
，试将相关知识点
推荐套卷
(本题满分14分) 若F1、F2为双曲线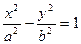的左、右焦点，O为坐标原点，P在双曲线左支上，M在右准线上，且满足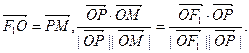（Ⅰ）求此双曲线的离心率；（Ⅱ）若此双曲线过点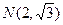，求双曲线方程；（Ⅲ）设（Ⅱ）中双曲线的虚轴端点为B1，B2（B1在y轴正半轴上），求B2作直线AB与双曲线交于A、B两点，求时，直线AB的方程.
粤公网安备 44130202000953号