(本小题满分12分)
已知B ,C分别为 函数y=Asinωx  在y轴右侧的第一个最大值点和最小值点,O为原点,若
在y轴右侧的第一个最大值点和最小值点,O为原点,若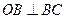 ,且
,且 (1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间
(1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间
相关知识点
推荐套卷
(本小题满分12分)
已知B ,C分别为 函数y=Asinωx  在y轴右侧的第一个最大值点和最小值点,O为原点,若
在y轴右侧的第一个最大值点和最小值点,O为原点,若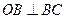 ,且
,且 (1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间
(1) 求A ,ω 的值 (2)求函数y=Asinωx 的单调递增区间