某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元),求随机变量
(元),求随机变量 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
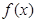 =
=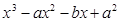 ,
,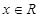 ,
,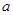 ,
,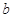 为常数。
为常数。 =1处有极值10,求实数
=1处有极值10,求实数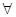
 的方程为
的方程为 ,直线
,直线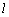 的方程为
的方程为 ,点
,点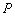 在直线
在直线 ,切点为
,切点为 .
. ,试求点
,试求点 点的坐标为
点的坐标为 ,过
,过 两点,当
两点,当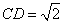 时,求直线
时,求直线 的方程
的方程 三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。 ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
 ,短轴长为8,
,短轴长为8, 作倾斜角为
作倾斜角为 的直线交椭圆C于A、B两点,求
的直线交椭圆C于A、B两点,求 的面积。
的面积。
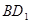 ∥平面
∥平面 ;
; 平面
平面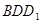 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号