已知函数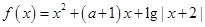
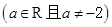 ,且
,且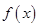 能表示成一个奇函数
能表示成一个奇函数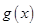 和一个偶函数
和一个偶函数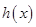 的和.
的和.
(1)求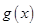 和
和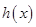 的解析式.
的解析式.
(2)命题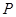 :函数
:函数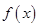 在区间
在区间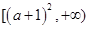 上是增函数;命题
上是增函数;命题 :函数
:函数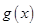 是减函数,如果命题
是减函数,如果命题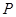 、
、 有且仅有一个是真命题,求实数
有且仅有一个是真命题,求实数 的取值范围.
的取值范围.
(3)在(2)的条件下,比较 和
和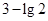 的大小.
的大小.
相关知识点
推荐套卷
已知函数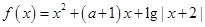
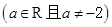 ,且
,且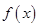 能表示成一个奇函数
能表示成一个奇函数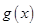 和一个偶函数
和一个偶函数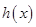 的和.
的和.
(1)求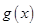 和
和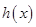 的解析式.
的解析式.
(2)命题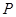 :函数
:函数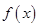 在区间
在区间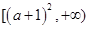 上是增函数;命题
上是增函数;命题 :函数
:函数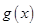 是减函数,如果命题
是减函数,如果命题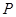 、
、 有且仅有一个是真命题,求实数
有且仅有一个是真命题,求实数 的取值范围.
的取值范围.
(3)在(2)的条件下,比较 和
和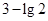 的大小.
的大小.