在矩形ABCD中，点P在AD上，AB=2，AP=1，将三角板的直角顶点放在点P处，三角板的两直角边分别能与AB、BC边相交于点E、F，连接EF．
（1）如图，当点E与点B重合时，点F恰好与点C重合，求此时PC的长；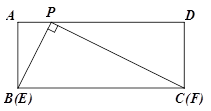
（2）将三角板从（1）中的位置开始，绕点P顺时针旋转，当点E与点A重合时停止，在这个过程中，请你观察、探究并解答：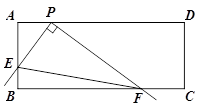
①∠PEF的大小是否发生变化？请说明理由；
②直接写出从开始到停止，线段EF的中点所经过的路线长．
相关试题
的两个实数根，不解方程，求下列代数式的值.[xx|k.Co
）（
）
阅读材料：为解方程（x2－1）2－5（x2－1）＋4＝0，我们可以将x2－1看作一个整体，然后设x2－1＝y……①，那么原方程可化为y2－5y＋4＝0，解得y1＝1，y2＝4．当y＝1时，x2－1＝1，∴x2＝2，∴x＝±
；当y＝4时，x2－1＝4，∴x2＝5，∴x＝±
，故原方程的解为x1＝，x2＝
，x3＝，x4＝
．
解答问题：（1）上述解题过程，在由原方程得到方程①的过程中，利用_________法达到了解方程的目的，体现了转化的数学思想；
（2）请利用以上知识解方程x4－x2－6＝0．
的一元二次方程
．
取何值，方程总有两个不相等的实数根；相关知识点
推荐套卷
粤公网安备 44130202000953号