(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为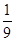 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为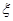 ,试写出
,试写出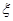 的分布列,并求
的分布列,并求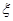 的数学期望。
的数学期望。
相关知识点
推荐套卷
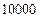 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在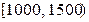 ).
).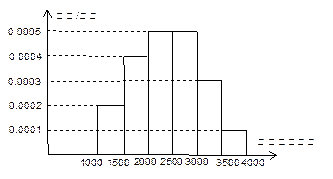
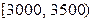 的频率;
的频率; 人作进一步分析,则月收入在
人作进一步分析,则月收入在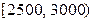 的这段应
的这段应 出多少人?
出多少人? 在
在 与
与 时都取得极值.
时都取得极值.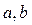 的值;
的值;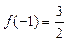 ,求
,求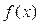 的单调区间和极值.
的单调区间和极值. ,求
,求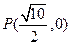 作倾斜角为
作倾斜角为 的直线与曲线
的直线与曲线 交于点
交于点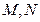 ,
, 的最小值及相应的
的最小值及相应的 .
. 的解集;
的解集;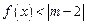 的解集是非空的集合,求实数
的解集是非空的集合,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号