一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为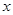 (时),两车之间的距离为
(时),两车之间的距离为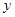 (千米),图中的折线表示从两车出发至快车到达乙地过程中
(千米),图中的折线表示从两车出发至快车到达乙地过程中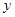 与
与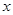 之间的函数关系.
之间的函数关系.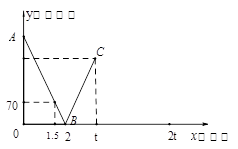
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中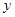 关于
关于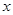 的函数的大致图象.
的函数的大致图象.
相关知识点
推荐套卷

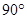 ,说明四边形ABCD有外接圆.
,说明四边形ABCD有外接圆.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号