已知二次函数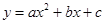 的图象经过点A(3,0),B(2,-3),C(0,-3).
的图象经过点A(3,0),B(2,-3),C(0,-3).
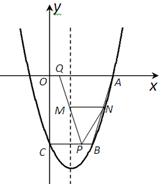
(1)求此函数的解析式及图象的对称轴;
(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动,点Q从O点出发以相同的速度沿线段OA向A点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.
①当t为何值时,四边形ABPQ为等腰梯形;
②设PQ与对称轴的交点为M,过M点作x轴的平行线交AB于点N,设四边形ANPQ的面积为S,求面积S关于时间t的函数解析式,并指出t的取值范围;当t为何值时,S有最大值或最小值.