（本小题满分12分）
设平面直角坐标系
中，设二次函数
的图象与两坐标轴有三个交点，经过这三个交点的圆记为
．求：
（Ⅰ）求实数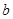
的取值范围；
（Ⅱ）求圆的方程；
（Ⅲ）问圆是否经过某定点（其坐标与b 无关）？请证明你的结论．
相关试题
，
的图像；（2）解不等式
。
是定义在
上的减函数，并且满足
，
，
的值， （2）如果
，求x的取值范围。
是定义在R上的函数，
，
。
.
上画出函数
的图像；
时，求证：在区间
上，
的图像位于函数
，（1）求函数的定义域；（2）求
的单调区间；推荐套卷
（本小题满分12分）
设平面直角坐标系中，设二次函数的图象与两坐标轴有三个交点，经过这三个交点的圆记为．求：
（Ⅰ）求实数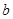的取值范围；
（Ⅱ）求圆的方程；
（Ⅲ）问圆是否经过某定点（其坐标与b 无关）？请证明你的结论．
粤公网安备 44130202000953号