如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H。
（1）求直线AC的解析式；
（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设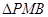
的面积为
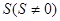，点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；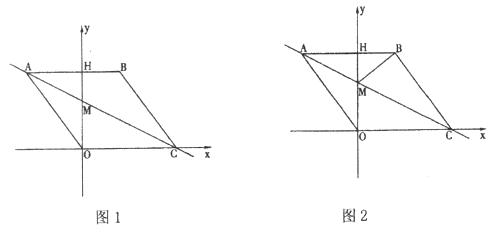
相关试题
与一次函数y=kx﹣2的图象都经过点A（a，﹣4），且一次函数y=kx﹣2的图象与x轴交于点B．相关知识点
推荐套卷
如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H。
（1）求直线AC的解析式；
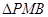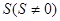（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设的面积为，点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
粤公网安备 44130202000953号