如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设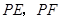 与
与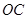 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线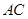 所对应的函数关系式;
所对应的函数关系式;
(2)当点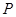 是线段
是线段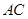 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点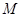 到
到 轴的距离
轴的距离 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点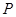 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.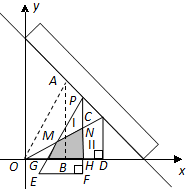
相关知识点
推荐套卷
 的值.
的值.
 的值;
的值; 为
为 上任意一点,以
上任意一点,以 ,
, 为边作□
为边作□ .试求对角线
.试求对角线 长的最小值和PQ最小时
长的最小值和PQ最小时
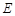 ,使
,使 ,再以
,再以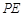 ,
,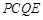 .请直接写出对角线
.请直接写出对角线


 粤公网安备 44130202000953号
粤公网安备 44130202000953号