（本小题满分12分）某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，这两族人数占各自小区总人数的比例如下：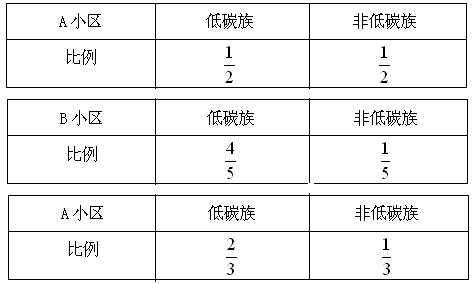
（1）从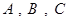
三个社区中各选一人，求恰好有2人是低碳族的概率；
（2）在B小区中随机选择20户，从中抽取的3户中“非低碳族”数量为X，求X的分布列和期望EX.
的定义域和值域.
;
+2cosx.
.
.
，若方程mcosx-1=cosx+m有解，试求参数m的取值范围.相关知识点
推荐套卷
（本小题满分12分）某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，这两族人数占各自小区总人数的比例如下：
（1）从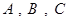三个社区中各选一人，求恰好有2人是低碳族的概率；
（2）在B小区中随机选择20户，从中抽取的3户中“非低碳族”数量为X，求X的分布列和期望EX.
粤公网安备 44130202000953号