在平面直角坐标系
中,曲线
的参数方程为
(
为参数)曲线
的参数方程为
(
,
为参数)在以
为极点,
轴的正半轴为极轴的极坐标系中,射线
:
与
,
各 有一个交点.当
时,这两个交点间的距离为
,当
时,这两个交点重合。
有一个交点.当
时,这两个交点间的距离为
,当
时,这两个交点重合。
(I)分别说明
,
是什么曲线,并求出
与
的值;
(II)设当
时,
与
,
的交点分别为
,
,当
时,
与
,
的交点为
,
,求四边形
的面积。
相关知识点
推荐套卷
 ,
,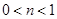 ;命题
;命题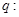 关于
关于 的方程
的方程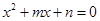 有两个小于1的正根 .试分析
有两个小于1的正根 .试分析 是
是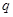 的什么条件 .
的什么条件 .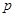 ,则
,则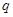 ”的形式,并写出它的逆命题、否命题与逆否命题,并分别判断其真假 .
”的形式,并写出它的逆命题、否命题与逆否命题,并分别判断其真假 .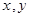 满足
满足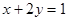 ,求
,求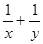 的最小值有如下解法:
的最小值有如下解法: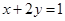 且
且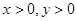 .
.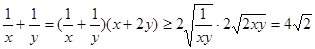
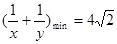 .
. 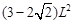 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号