已知点P在圆x2＋y2＝1上运动，过点P作x轴的垂线，垂足为D，点M在DP的延长线上，且有|DP|＝|MP|.(1)求M点的轨迹方程C；(2)已知直线l过点(0，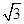
)，且斜率为1，求l与C相交所得的弦长．
，
，且
，
，
的值.
，
的奇偶性；（2）证明
．
．
，求它的焦点坐标和准线方程．
，求
的值．相关知识点
推荐套卷
已知点P在圆x2＋y2＝1上运动，过点P作x轴的垂线，垂足为D，点M在DP的延长线上，且有|DP|＝|MP|.(1)求M点的轨迹方程C；(2)已知直线l过点(0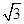，)，且斜率为1，求l与C相交所得的弦长．
粤公网安备 44130202000953号