三棱柱ABC－A1B1C1在如图所示的空间直角坐标系中，已知AB＝2，AC＝4，A1A＝3.D是BC的中点．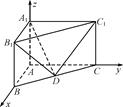
(1)求直线DB1与平面A1C1D所成角的正弦值；
(2)求二面角B1-A1D-C1的正弦值．
是R上的奇函数，且当
时，
在区间[1,3]上有最大值5和最小值2，求
的值
|
或
}，B＝{
或
}，若
，求实数
的取值范围．
，
，求
的值
，对任意
，恒有
．
，
，
的值；
在
上的最值．相关知识点
推荐套卷
三棱柱ABC－A1B1C1在如图所示的空间直角坐标系中，已知AB＝2，AC＝4，A1A＝3.D是BC的中点．
(1)求直线DB1与平面A1C1D所成角的正弦值；
(2)求二面角B1-A1D-C1的正弦值．
粤公网安备 44130202000953号