我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,
即已知三角形的三边长,求它的面积.用现代式子表示即为: ……①(其中
……①(其中 、
、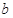 、
、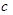 为三角形的三边长,
为三角形的三边长,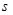 为面积).
为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式: ……②(其中
……②(其中 ).
).
⑴ 若已知三角形的三边长分别为5、7、8,试分别运用公式①和公式②,计算该三角形的面积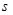 ;
;
⑵ 你能否由公式①推导出公式②?请试试.
相关知识点
推荐套卷
我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,
即已知三角形的三边长,求它的面积.用现代式子表示即为: ……①(其中
……①(其中 、
、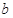 、
、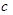 为三角形的三边长,
为三角形的三边长,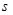 为面积).
为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式: ……②(其中
……②(其中 ).
).
⑴ 若已知三角形的三边长分别为5、7、8,试分别运用公式①和公式②,计算该三角形的面积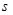 ;
;
⑵ 你能否由公式①推导出公式②?请试试.