如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.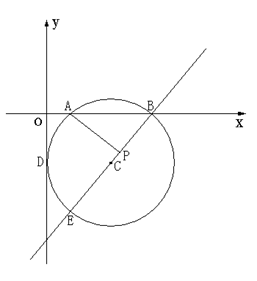
⑴ 求点C的坐标;
⑵ 连结BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BP·BE,能否推出AP⊥BE?请给出你的结论,并说明理由;
⑶ 在直线BE上是否存在点Q,使得AQ2=BQ·EQ?若存在,求出点Q的坐标;若不存在,也请说明理由.
相关知识点
推荐套卷
如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
⑴ 求点C的坐标;
⑵ 连结BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BP·BE,能否推出AP⊥BE?请给出你的结论,并说明理由;
⑶ 在直线BE上是否存在点Q,使得AQ2=BQ·EQ?若存在,求出点Q的坐标;若不存在,也请说明理由.