（本题10分）袋中有红、白两种颜色的小球共7个，它们除颜色外完全相同，从中任取2个，都是白色小球的概率为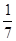
，甲、乙两人不放回地从袋中轮流摸取一个小球，甲先取，乙后取，然后再甲取……，直到两人中有一人取到白球时游戏停止，用X表示游戏停止时两人共取小球的个数。
（1）求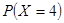
；
（2）求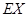
。
相关试题
为实数，函数
，
．
的奇偶性；（2）求 
是定义在
上的奇函数，当
时，
，
.
在
上是增函数.
，集合
，
.
.
（闭区间[m，n]的长度定义为n –m）．
是否存在实数根？说明理由。相关知识点
推荐套卷
（本题10分）袋中有红、白两种颜色的小球共7个，它们除颜色外完全相同，从中任取2个，都是白色小球的概率为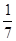，甲、乙两人不放回地从袋中轮流摸取一个小球，甲先取，乙后取，然后再甲取……，直到两人中有一人取到白球时游戏停止，用X表示游戏停止时两人共取小球的个数。
（1）求；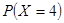
（2）求。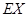
粤公网安备 44130202000953号