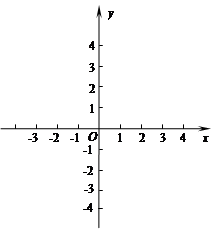(1)用配方法把二次函数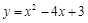 化为顶点式,并在直角坐标系中画出它的大致图象(
化为顶点式,并在直角坐标系中画出它的大致图象(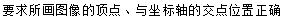 ).
).
(2)若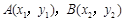 是函数
是函数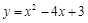 图象上的两点,且
图象上的两点,且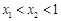 ,请比较
,请比较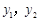 的大小关系.(直接写结果)
的大小关系.(直接写结果)
(3)把方程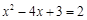 的根在函数
的根在函数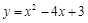 的图象上表示出来.
的图象上表示出来.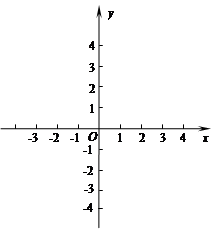
相关知识点
推荐套卷
(1)用配方法把二次函数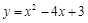 化为顶点式,并在直角坐标系中画出它的大致图象(
化为顶点式,并在直角坐标系中画出它的大致图象( ).
).
(2)若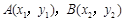 是函数
是函数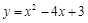 图象上的两点,且
图象上的两点,且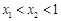 ,请比较
,请比较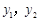 的大小关系.(直接写结果)
的大小关系.(直接写结果)
(3)把方程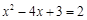 的根在函数
的根在函数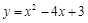 的图象上表示出来.
的图象上表示出来.