如图9,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF。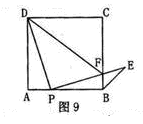
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
相关知识点
推荐套卷
如图9,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF。
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.