如图,直线AB与CD相交于点O, OP是∠BOC的平分线,OE⊥AB,OF⊥CD.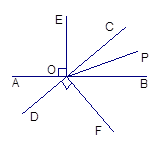
(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°,
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP=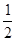 ∠ = 度.
∠ = 度.
③求∠POF的度数.
如图,直线AB与CD相交于点O, OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°,
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP=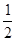 ∠ = 度.
∠ = 度.
③求∠POF的度数.