如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O 的切线交直线AC于点D,点E为CH的中点,连结并延交BD于点F,直线CF交AB的延长线于G.
⑴求证:AE·FD=AF·EC;
⑵求证:FC=FB;
⑶若FB=FE=2,求⊙O 的半径r的长.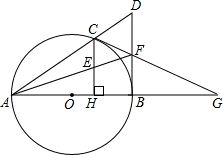
相关知识点
推荐套卷
如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O 的切线交直线AC于点D,点E为CH的中点,连结并延交BD于点F,直线CF交AB的延长线于G.
⑴求证:AE·FD=AF·EC;
⑵求证:FC=FB;
⑶若FB=FE=2,求⊙O 的半径r的长.