小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________㎝,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?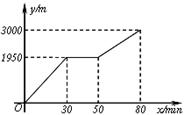
相关知识点
推荐套卷
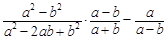 ,其中
,其中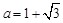 ,
,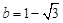 .
.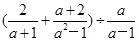 ,其中
,其中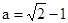 .
.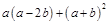 ,其中
,其中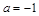 ,
,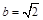 .
.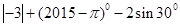
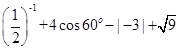
 粤公网安备 44130202000953号
粤公网安备 44130202000953号