齐齐哈尔市教育局非常重视学生的身体健康状况,为此在体育考试中对部分学生的立定跳远成绩进行了调查(分数为整数,满分100分),根据测试成绩(最低分为53分)分别绘制了如下统计表和统计图.(如图)
分数
|
59.5分以下
|
59.5分以上
|
69.5分以上
|
79.5以上
|
89.5以上
|
人数
|
3
|
42
|
32
|
20
|
8
|
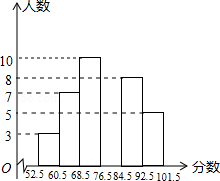
(1)被抽查的学生为 人.
(2)请补全频数分布直方图.
(3)若全市参加考试的学生大约有4500人,请估计成绩优秀的学生约有多少人?(80分及80分以上为优秀)
(4)若此次测试成绩的中位数为78分,请直接写出78.5~89.5分之间的人数最多有多少人?.