某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元．大樱桃售价为每千克40元，小樱桃售价为每千克16元．
（1）大樱桃和小樱桃的进价分别是每千克多少元？销售完后，该水果商共赚了多少元钱？
（2）该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了 ．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的 ，大樱桃的售价最少应为多少？
相关试题
如图，用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD，其中，NH=NG=1cm，设BF=acm．
（1）用含a的代数式表示CE= cm，DE= cm；
（2）求长方形ABCD的周长．（用含a的代数式表示）
，0，3.14，﹣
，﹣0.55，8，﹣2．
）
x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
相关知识点
推荐套卷
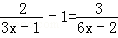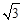粤公网安备 44130202000953号