在平面直角坐标系内，已知点A(0，6)、点B(8，0)，动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．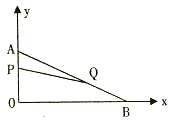
(1)求直线AB的解析式；
(2)当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时，求四边形OPQB的面积．
与
相交于点
，
平分
，
， 
，
，试说明：
∥
．
，其中
相关知识点
推荐套卷
在平面直角坐标系内，已知点A(0，6)、点B(8，0)，动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．
(1)求直线AB的解析式；
(2)当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时，求四边形OPQB的面积．
粤公网安备 44130202000953号