某班同学利用节假日进行社会实践，在25~ 55岁的人群中随机抽取n人进行了一次关于生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”．根据调查结果得到如下统计表和各年龄段人数频率分布直方图：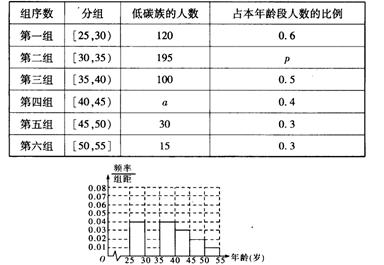
（I）补全频率分布直方图并求n，a，p的值；
（Ⅱ）从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁年龄段的人数为X，求X的分布列和数学期望．
相关试题
}的前
项和为
，且满足
，
．
}是等差数列；
，求证：
．
， 
满足条件：
， 
．
是等比数列，并求数列
项和
，并求使得
对任意
N*都成立的正整数
的最小值．
、
、
分别为
的三边
、
、
所对的角，向量
，
，且
.
，求边
}中，
，前
项和
．
项、第
项、第
项…第
项……按原来的顺序组成一个新的数列{
}，求数列{
项和
．
，
，
.
//
，求证：ΔABC为等腰三角形；
，边长
，角
，求ΔABC的面积 .相关知识点
推荐套卷
粤公网安备 44130202000953号