如图，一矩形铁皮的长为8cm，宽为5cm，在四个角上
截去四个相同的小正方形，制成一个无盖的小盒子.
（1）将小盒子的容积V写成关于小正方形的边长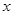
的函数；
（2）正方形的边长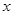为多少时，盒子容积最大？求出最大值.
相关试题
；
．由以上两式成立，你能得到一个什么的推广？证明你的结论.
对一切正整数
都成立，求正整数
的最大值，并证明结论．
，
（其中
，且
）．
请你推测
能否用
来表示；
中，
，若
，则
；若类比该命题，如图（2），三棱锥
中，
面
点在三角形
所在平面内的射影为
，则有什么结论？命题是否是真命题．
相关知识点
推荐套卷
如图，一矩形铁皮的长为8cm，宽为5cm，在四个角上
截去四个相同的小正方形，制成一个无盖的小盒子.
（1）将小盒子的容积V写成关于小正方形的边长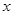的函数；
（2）正方形的边长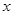为多少时，盒子容积最大？求出最大值.
粤公网安备 44130202000953号