随机抽取某厂的某种产品100件,经质检,其中有一等品63件、二等品25件、三等品10件、次品2件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为 .
.
(1)求 的分布列;
的分布列;
(2)求1件产品的平均利润(即 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为 ,一等品率提高为
,一等品率提高为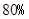 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
相关知识点
推荐套卷
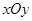 中,点
中,点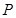 到两点
到两点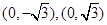 的距离之和为4,设点
的距离之和为4,设点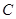 ,直线
,直线 与
与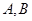 两点.
两点.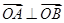 ,求
,求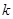 的值
的值 与析出银的光学密度
与析出银的光学密度 由公式
由公式 表示,现测得试验数据如下:
表示,现测得试验数据如下:

 -2.30,Ln0.37
-2.30,Ln0.37 ,
, ,
, )
) )n的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的5/6.
)n的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的5/6.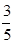 .
.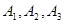 还喜欢打羽毛球,
还喜欢打羽毛球,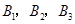 还喜欢打乒乓球,
还喜欢打乒乓球,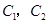 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求女生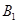 和
和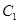 至少被选中一名的概率.
至少被选中一名的概率.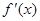 =6x-2,数列{
=6x-2,数列{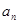 }的前n项和为
}的前n项和为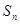 ,点(n,
,点(n,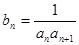 ,
,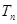 是数列{
是数列{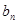 }的前n项和,求使得
}的前n项和,求使得 粤公网安备 44130202000953号
粤公网安备 44130202000953号