如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H.
(1)①直接写出点E的坐标: .
②求证:AG=CH.
(2)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式.
(3)在(2)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
相关知识点
推荐套卷
 的图象与函数
的图象与函数 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.
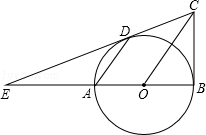
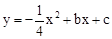 与x轴交于点A(2,0),交y轴于点B(0,
与x轴交于点A(2,0),交y轴于点B(0,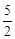 ).直线
).直线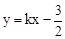 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.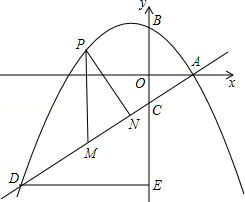
 粤公网安备 44130202000953号
粤公网安备 44130202000953号