2005年某市的空气质量状况分布如下表:
| 污染指数X |
30 |
60 |
100 |
110 |
130 |
140 |
| P |
 |
 |
 |
 |
 |
 |
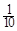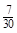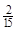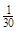其中X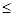
50时，空气质量为优，
时空气质量为良，
时，空气质量为轻微污染。（1）求E（X）的值；（2）求空气质量达到优或良的概率。
相关试题
，其中
.
时，求
在
上的最大值;
时，函数
，求函数
的内角
、
、
所对的边分别为
、
、
，且
.
，求
的取值范围.
的等差数列
中，
，
、
、
成等比数列;
满足
，求数列
，
，
。
上的单调递减区间.
（其中
，
是自然对数的底数，
）．
时，求函数
的极值；
恒成立，求实数
的取值范围；
，都有
．相关知识点
推荐套卷
2005年某市的空气质量状况分布如下表:
| 污染指数X |
30 |
60 |
100 |
110 |
130 |
140 |
| P |
|
|
|
|
|
|
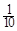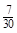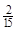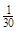其中X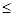50时，空气质量为优，时空气质量为良，时，空气质量为轻微污染。（1）求E（X）的值；（2）求空气质量达到优或良的概率。
粤公网安备 44130202000953号