已知:如图,四边形ABCD是关于坐标原点中心对称的四边形,其中点A B
B ,反比例函数
,反比例函数 经过点A.
经过点A.
(1)求反比例函数.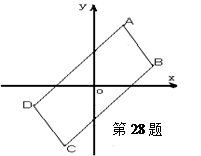
(2)设直线 经过C、D两点,在原有坐标系中画出并利用函数的图象,
经过C、D两点,在原有坐标系中画出并利用函数的图象,
直接写出不等式 的解集为: .
的解集为: .
相关知识点
推荐套卷
已知:如图,四边形ABCD是关于坐标原点中心对称的四边形,其中点A B
B ,反比例函数
,反比例函数 经过点A.
经过点A.
(1)求反比例函数.
(2)设直线 经过C、D两点,在原有坐标系中画出并利用函数的图象,
经过C、D两点,在原有坐标系中画出并利用函数的图象,
直接写出不等式 的解集为: .
的解集为: .