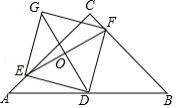
如图，在等腰直角三角形 中， ， ， 是 的中点， ， 分别是 ， 上的点（点 不与端点 ， 重合），且 ，连接 并取 的中点 ，连接 并延长至点 ，使 ，连接 ， ， ， ．
（1）求证：四边形 是正方形；
（2）当点 在什么位置时，四边形 的面积最小？并求四边形 面积的最小值．
相关试题
（本题8分）某水果销售点用1000元购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：
| 进价（元/千克） |
售价（元/千克） |
|
| 甲种 |
5 |
8 |
| 乙种 |
9 |
13 |
（1）这两种水果各购进多少千克？
（2）若该水果店按售价销售完这批水果，获得的利润是多少元？
（本题8分）某学校举行“社会主义核心价值观”知识比赛活动，全体学生都参加比赛，学校对参赛学生均给与表彰，并设置一、二、三等奖和纪念奖共四个奖项，赛后将获奖情况绘制成如下所示的两幅不完整的统计图，请根据图中所给的信息，解答下列问题：
（1）该校共有名学生；
（2）在图1中，“三等奖”随对应扇形的圆心角度数是；
（3）将图2补充完整；
（4）从该校参加本次比赛活动的学生中随机抽查一名．求抽到获得一等奖的学生的概率．
（本题8分）如图，在△
中，
，点
在
的延长线上．
（1）按下列要求作图，并在图中标明相应的字母．
①作
的平分线
；
②作
的中点
，连接
，并延长交于点
，连接
．
（2）在（1）的条件下，判断四边形
的形状．并证明你的结论．
，其中
．
经过点（1，﹣1），且对称轴为在线
，点P、Q均在抛物线上，点P位于对称轴右侧，点Q位于对称轴左侧，PA垂直对称轴于点A，QB垂直对称轴于点B，且QB=PA+1，设点P的横坐标为
．
（
）经过Q、B、P三点，若其对称轴把四边形PAQB分成面积为1：5的两部分，直接写出此时相关知识点
推荐套卷
粤公网安备 44130202000953号